شروع سرمایه‌گذاری در سهام – قسمت سی و هفتم
ریحانه لاریجانی
کارشناس توسعه فرهنگ سرمایه‌گذاری بورس تهران
در پاسخ به این پرسش که چه میزان ریسک در ازای چه میزان بازدهی قابل‌قبول است، توضیحاتی در مورد آشنایی با ریسک و تعاریف آن بیان شد. در این قسمت، در خصوص اندازهگیری ریسک توضیحاتی ارائه خواهد شد.
چگونه می‌توان ریسک را اندازهگیری کرد؟
با کمک علم آمار می‌توان مقدار کمّی ریسک یک دارایی را اندازهگیری نمود. نحوه اندازهگیری تغییر‌پذیری ریسک دارایی (بازده یک دارایی) با کمک دو آماره انحراف معیار و ضریب تغییرات در زیر توضیح داده شده است.
اندازهگیری ریسک یک دارایی از طریق انحراف معیار:
متداول‌ترین شاخص آماری که برای محاسبه ریسک یک دارایی مورد استفاده قرار می‌گیرد، انحراف معیار است که میزان پراکندگی بازده‌های یک دارایی را حول بازده مورد‌انتظار، اندازهگیری می‌کند. بازده مورد‌انتظار، میزان بازده‌ای است که یک دارایی به احتمال قوی خواهد داشت. این بازده از طریق زیر محاسبه می‌شود:
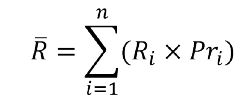
در رابطه فوق:
فرمول محاسبه انحراف معیار بازده به‌صورت زیر است:
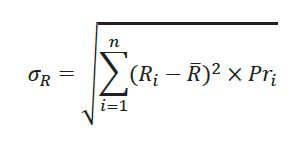
مثال: در جدول زیر، بازده مورد‌انتظار دارایی‌های A و B شرکت الف نشان داده شده است. n برابر ۳ است (حالت خوش‌بینانه، بدبینانه، بیشترین احتمال). در ستون اول جدول، مقادیر احتمال وقوع وضعیت و در ستون دوم، میزان بازده برای این دو دارایی ذکر شده است. بازده مورد‌انتظار هر دوی این دارایی‌ها ۱۵درصد است. انحراف معیار بازده‌ها چقدر است؟
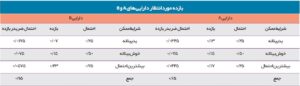
در ادامه، انحراف معیار بازده دارایی A و B محاسبه شده است:
انحراف معیار بازده دارایی A:
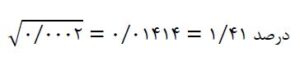
انحراف معیار بازده دارایی B:
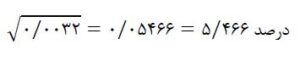
به‌طور کلی، هرچه انحراف معیار بیشتر باشد، ریسک بیشتر است.
بازده دارایی B دارای انحراف معیار ۵/۴۶۶ درصد است که از انحراف معیار بازده دارایی A 1/41 درصد بیشتر است و در نتیجه، دارایی B در مقایسه با دارایی A، ریسک بیشتری دارد.
اندازهگیری ریسک یک دارایی از طریق ضریب تغییرات:
ضریب تغییرات معیاری برای اندازهگیری پراکندگی است. این ضریب برای مقایسه ریسک دارایی‌هایی که بازده‌های مورد‌انتظارشان با یکدیگر متفاوت است، مفید می‌باشد.
محاسبه ضریب تغییرات بازده:
هرچه ضریب تغییرات بزرگتر باشد، میزان ریسک نیز بیشتر است. در مورد دارایی‌های A وB می‌توان ضریب تغییرات بازده را به‌صورت زیر محاسبه کرد:
ضریب تغییرات بازده دارایی A:
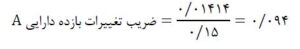
ضریب تغییرات بازده دارایی B:
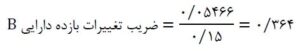
همان‌طور که در مثال بالا مشاهده شد ضریب تغییرات بازده دارایی B بیشتر از دارایی A است، بنابراین می‌توان نتیجه گرفت دارایی B ریسک بیشتری دارد.
